√100以上 tree(3) vs graham's number 428715-Tree(3) vs graham's number

Graham's Number used to be the biggest number I could name, but now I understand that TREE (3) ( https//enwikipediaorg/wiki/Kruskal%27s_tree_theorem ) is bigger still by a truly incredible amount (and TREE (1) = 1, and TREE (2) = 3) Unfortunately I don't understand that Wiki pageReply mrsmspin on March 26, 17 at 1031 pmThe Graham number is a figure that measures a stock's fundamental value by taking into account the company's earnings per share and book value per share The Graham number is the upper bound of

How Big Is The Number Tree 3 Let Us See How Big A Forest Can We Grow By Priyabrata Biswas Towards Data Science

Tree(3) vs graham's number

Tree(3) vs graham's number-TREE(3) is indistinguishable from zero compared to Loader's number1, which basically takes every bit pattern up to some n and expresses this as a program in the Calculus of Constructions This system is a bit weaker than being Turing complete, but the programs do always terminate (this makes the number computable compared with, say, the Busy Beaver number which does a similar thing with Turing complete programs)Later on, Graham showed that the upper bound to for this riddle is much much smaller than Graham's number, but still huge TREE(3) Equations aren't just useful' they're often beautiful

How Big Is The Number Tree 3 Let Us See How Big A Forest Can We Grow By Priyabrata Biswas Towards Data Science

Graham's Number – literally big enough to collapse your head into a black hole Graham's Number is a number so big that it would literally collapse your head into a black hole were you fully able to comprehend it And that's not hyperbole – the informational content of Graham's Number is so astronomically large that it exceeds the maximum amount of entropy that could be stored in aIt seems the Arildno number is a dwarf, after allTREE(3) is indistinguishable from zero compared to Loader's number1, which basically takes every bit pattern up to some n and expresses this as a program in the Calculus of Constructions This system is a bit weaker than being Turing complete, but the programs do always terminate (this makes the number computable compared with, say, the Busy Beaver number which does a similar thing with Turing complete programs)

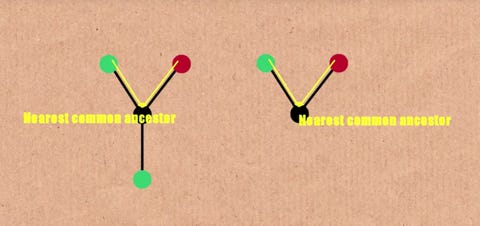
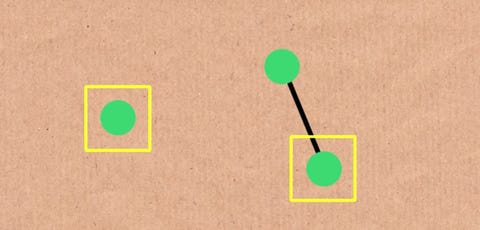
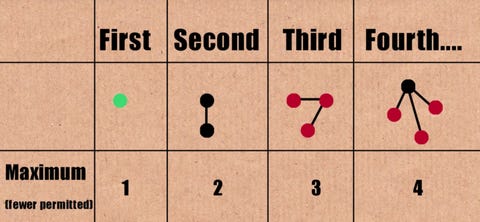
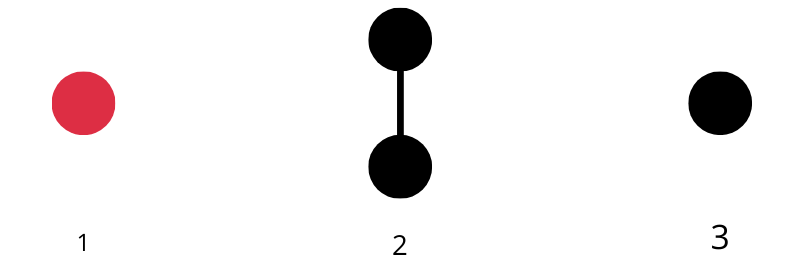
These rules guarantee that the resulting longest tree sequence is finite When the input is 1 or 2, the length of the longest possible tree is small When it is 3, the length is VERY VERY VERY long TREE(3) dwarfs big numbers like Graham's number Big numbers like Graham's number are impossibly big, bigger than our universeGraham's number is an immense number that arose as an upper bound on the answer of a problem in the mathematical field of Ramsey theoryIt is named after mathematician Ronald Graham, who used the number in conversations with popular science writer Martin Gardner as a simplified explanation of the upper bounds of the problem he was working on In 1977, Gardner described the number in ScientificIf you replaced all the 3 's in the construction of Graham's number with TREE (3), the resulting number would be smaller than g T R E E (3) where g n denotes the n th number in Graham's sequence with g 64 being Graham's number This is much much smaller than TREE (4), for example

Given that, apparently TREE (1)=1 and TREE (2)=3, it seems quite surprising that TREE (3) should suddenly be far greater than Graham's Number, but there it is Just so you know, one way of expressing it is TREE (3)> {3,6,3 1 1¬1,222} That's enough of that, eh?TREE (3) is way beyond the scope of Grahams Number You couldnt even begin to express TREE (3) in any way besides the Fast Growing hierarchy Grahams number is only between f omega1 (63) and f omega1 (64) TREE (3) is beyond the gamma 0 of the hierarchy, which is way bigger than the omegasSo the first step of the Graham's function, 3↑↑↑↑3 = g 1, is very roughly A(6,6) The second step g 2 is roughly A(g 1,g 1) and the actual Graham's number, g 64, is roughly A(g 63,g 63) That's how big Graham's number is You can also use the iterated function notation with the Ackermann function to approximate Graham's number more

Graham S Number Escalates Quickly Numberphile Youtube

Tony Padilla Jft96 Don T Buy The S N This Is Me And Hendo At The Cup Final Last Year Before He Got Ill I Will Tweet Back Graham S Number

Graham's Number Graham's number is connected to the following problem in the branch of mathematics known as Ramsey Theory Consider an ndimensional hypercube, and connect each pair of vertices to obtain a complete graph on 2 n vertices Then colour each of the edges of this graph either red or blueSo the first step of the Graham's function, 3↑↑↑↑3 = g 1, is very roughly A(6,6) The second step g 2 is roughly A(g 1,g 1) and the actual Graham's number, g 64, is roughly A(g 63,g 63) That's how big Graham's number is You can also use the iterated function notation with the Ackermann function to approximate Graham's number moreIn fact, $TREE(3)$ is a complete other league !

Wrap Your Head Around The Enormity Of The Number Tree 3

Www Canr Msu Edu Monroe Uploads Files May network 19 Pdf

Hello there This is Numberphile We mainly post videos about mathematics and just numbers in generalBut there's a huge difference between this problem and Graham's problem unlike the solution to Graham's problem, TREE(3) is not an upperbound It is known to be indeed be extremely huge, meaningActually, Graham's number is now considered pretty small by mathematicians For example, TREE(3) is so big that it makes Graham's number look like pretty much like zero in comparison The interesting thing about the TREE function is that it grows so rapidly eg TREE(1) = 1 TREE(2) = 3 TREE(3) = something insanely big!

Wrap Your Head Around The Enormity Of The Number Tree 3

How Many Zeros In A Million Billion And Trillion

Other specific integers (such as TREE(3)) known to be far larger than Graham's number have since appeared in many serious mathematical proofs, for example in connection with Harvey Friedman's various finite forms of Kruskal's theorem Additionally, smaller upper bounds on the Ramsey theory problem from which Graham's number derived have since been proven to be validWhile TREE (n) is at f θ ( Ω ω) ( n)!Using parentheses to emphasize the top down order 3 3 3 3 = 3 3 (3 3) = 3 3 27 =3 (3 27) = 3 7,625,597,484,987 = a 36 trilliondigit number Remember, a googol and its universefilling microscopic minisand is only a 100digit number

How Have Mathematicians Determined Tree 3 To Be Far Larger Than Graham Number Quora

Wrap Your Head Around The Enormity Of The Number Tree 3

My big numbers videos https//wwwyoutubecom/playlist?list=PLDewy_4QBpjtYjxNVVRNrSaAIBSAOkBH6 Which is bigger?Graham's Number Let be the smallest dimension of a hypercube such that if the lines joining all pairs of corners are twocolored for any , a complete graph of one color with coplanar vertices will be forced Stated colloquially, this definition is equivalent to considering every possible committee from some number of people and enumerating every pair of committeesGrahams Number, the largest number used in a mathematical proof (so large you cant even comprehend how $&%ing big it is), is a factor of 3 (Ie g1= 3^^^^3 using the ^ for the Knuth uparrow notation and grahams number = g64 where each step from g1 to 64 the number of arrows is iterated from the previous number, so g1 is incomprehensible and g2 has g1 number of ^'s and so on)

How Have Mathematicians Determined Tree 3 To Be Far Larger Than Graham Number Quora

Graham S Number Is Huge Tree3 Is Bigger Mathmemes

Sorry to tell you that, nesting of Graham's number for Graham's number times, G G ( 64) ( 64), doesn't come close to TREE (3) In fact, Graham's function G (n) is only at f ω 1 ( n) on FGH (Fast Growing Hierarchy);$\begingroup$ Pardon my ignorance, but isn't TREE(3) a finite number?Just as Graham's Number has not taken away from the googolplexes infamy as a really large number, later numbers such as TREE(3) will only add to the richness of the discussion Because of it's

Too Big To Write But Not Too Big For Graham Plus Maths Org

How Big Is The Number Tree 3 Let Us See How Big A Forest Can We Grow By Priyabrata Biswas Towards Data Science

Later on, Graham showed that the upper bound to for this riddle is much much smaller than Graham's number, but still huge TREE(3) Equations aren't just useful' they're often beautifulI watched the early number and counting video and it resonated so much with my experience with my 4year old daughter!As such, it can't possibly be larger than "any number expressible by iterations of n", can it?

From 1 000 000 To Graham S Number Wait But Why

Tree Vs Graham S Number Numberphile Youtube

Although the lower bound is larger than Graham's number, it's still at about the level ω1 in the fastgrowing hierarchy TREE (3), on the other hand, is higher than the Small Veblen Ordinal in the fastgrowing hierarchy, which is MUCH larger!And we can combinatorially show that TREE(3) ≥ n(4) (this inequality is in reality strict very strict, as n(4) is much closer to Graham's number than it is to TREE(3)) 34 shareThe number $n$ for which $G(n)>TREE(3)$ holds would be indistuinguishable from $TREE(3)$ itself If you know Conwaychains, they are usually unimaginably larger than Graham's number, for example $4\rightarrow 4\rightarrow 4\rightarrow 4$ is

Graham S Number Wikipedia

Largest Known Prime Number Wikipedia

The first two values are TREE1 = 1 and TREE2 = 3 The next value, TRE, is famously very large It vastly exceeds Graham's number and n n(5) (5) Chris Bird claimed that \(\text{TREE}3 > \{3, 6, 3 1 1 \neg 1,2 2 2\}\), using his array notationOther specific integers (such as TREE(3)) known to be far larger than Graham's number have since appeared in many serious mathematical proofs, for example in connection with Harvey Friedman's various finite forms of Kruskal's theorem Additionally, smaller upper bounds on the Ramsey theory problem from which Graham's number derived have since been proven to be validNo Unless I'm mistaken, Graham's number has a very specific meaning It is involved in a proof about colouring the edges of an ncube I don't remember the theorem, but Graham's number is the lowest number of dimensions in which that's dimension's respective hyper cube has some specific property which I forget

The Enormous Tree 3 Numberphile Youtube

No 3 Ltd V Pdv Insurance Co Aul Lawrence Graham

I don't recall how I learned these early math and honestly as a math teacher myself, I have been secretly worried about my daughter's progress Thanks Graham!His value for the upper bound on number of dimensions has been described by mathematicians as "fucking huge", and is known as Graham's number (His lower bound was 6, and this was bumped up to 13 in 08) Consider a sequence of numbers g n Each number of this sequence is in the form of 3 ↑ m 3, where m is some numberUsing parentheses to emphasize the top down order 3 3 3 3 = 3 3 (3 3) = 3 3 27 =3 (3 27) = 3 7,625,597,484,987 = a 36 trilliondigit number Remember, a googol and its universefilling microscopic minisand is only a 100digit number

Tree Vs Graham S Number Numberphile Youtube

Numberphile Love This Math Equivalent Of Batman Vs Superman Make Sure You Watch Both Parts T Co X8ecyr9knm T Co Drpaumcwvl T Co C86ikmvppd

Photograph Ron Graham juggles 4 balls, by Peter Vidor;Now I learnt about Graham's number from Numberphile which is probably where that Google search should have redirected you by now We obviously also know (from Numberphile) how off the scale if TREE(3) "It absolutely puts Graham's number to shame" is said in the video But my question is we know Graham's number is G(64)Graham's number is commonly celebrated as the largest number ever used in a serious mathematical proof, although much larger numbers have since claimed this title (such as TREE(3) and SCG(13)) The smallest Bowersism exceeding Graham's number is corporal , and the smallest Saibianism exceeding Graham's number is graatagold

Too Big To Write But Not Too Big For Graham Plus Maths Org

Is Tree 3 Bigger Than Graham S Number Quora

Graham's Number Graham's number is connected to the following problem in the branch of mathematics known as Ramsey Theory Consider an ndimensional hypercube, and connect each pair of vertices to obtain a complete graph on 2 n vertices Then colour each of the edges of this graph either red or blueAnd we can combinatorially show that TREE(3) ≥ n(4) (this inequality is in reality strict very strict, as n(4) is much closer to Graham's number than it is to TREE(3)) 34 shareAn enormous number beyond our ability to express with written notation, beyond what we could even begin to comprehend, bigger than the notoriously gargantuan Graham's number We know TREE(3

Tree 3 Is A Big Number I Mean Really Big Josh Kerr

1

A lower bound for n (4), and hence an extremely weak lower bound for TREE (3), is AA() (1), where A () is a version of Ackermann's function Graham's number, for example, is approximately A64 (4), which is much smaller than the lower bound AA() (1)Presented as research material on the topic of Big numbers for which Graham's number(s) is an ongoing inspirationProfessor Tony Padilla on the epic number, TREE(3) Continues at https//youtube/IihcNa9YAPkMore links & stuff in full description below ↓↓↓Graham's Number

My New Obsession Is Really Really Really Really Really Really Large Numbers And If You Think Graham S Number Is Astronomy Facts Looking Up Space And Astronomy

How Have Mathematicians Determined Tree 3 To Be Far Larger Than Graham Number Quora

Lavrov, Lee, Mackey "Graham's Number is Less Than 2^^^6" Konstantinos Tyros "On colorings of variable words" VIDEO Ron Graham explains bounds for Graham's Number;Other specific integers (such as TREE(3)) known to be far larger than Graham's number have since appeared in many serious mathematical proofs, for example in connection with Harvey Friedman's various finite forms of Kruskal's theorem Additionally, smaller upper bounds on the Ramsey theory problem from which Graham's number derived have since been proven to be validThe various "Graham's number"s The "GrahamRothschild Number" The "GrahamGardner Number" The "GrahamConway Number" Superclasses Conway's Chained Arrow Notation A In general, when naming 10 3 N 3, the rules above are to be used for each group of 3 digits in the number N

1

How Big Is The Number Tree 3 Let Us See How Big A Forest Can We Grow By Priyabrata Biswas Towards Data Science

Friedman proved that the function eventually dominates all recursive functions provably total in the system A C A0 π¹ 2 — BI The smallest nontrivian member of the sequence is the famously TREEWhat's amusing is that the above lower bound for TREE(3) is SO much smaller than TREE(3) that it gives people the wrong idea about it's size Although the lower bound is larger than Graham's number, it's still at about the level ω1 in the fastgrowing hierarchyGraham's Number used to be the biggest number I could name, but now I understand that TREE (3) ( https//enwikipediaorg/wiki/Kruskal%27s_tree_theorem ) is bigger still by a truly incredible amount (and TREE (1) = 1, and TREE (2) = 3) Unfortunately I don't understand that Wiki page

Graham S Number Don T Think Of This Number Your Brain Could Implode Into A Black Hole

Www2 Palomar Edu Pages Math Files 17 12 2 E Finitely Big Numbers Key Pdf

A lower bound for n (4), and hence an extremely weak lower bound for TREE (3), is AA() (1), where A () is a version of Ackermann's function Graham's number, for example, is approximately A64 (4), which is much smaller than the lower bound AA() (1)$\endgroup$ – Dylan Thurston Apr 12 '12 at 1158 2

How Big Is The Number Tree 3 Let Us See How Big A Forest Can We Grow By Priyabrata Biswas Towards Data Science

Graham Foundation About Newsletter

From 1 000 000 To Graham S Number Wait But Why

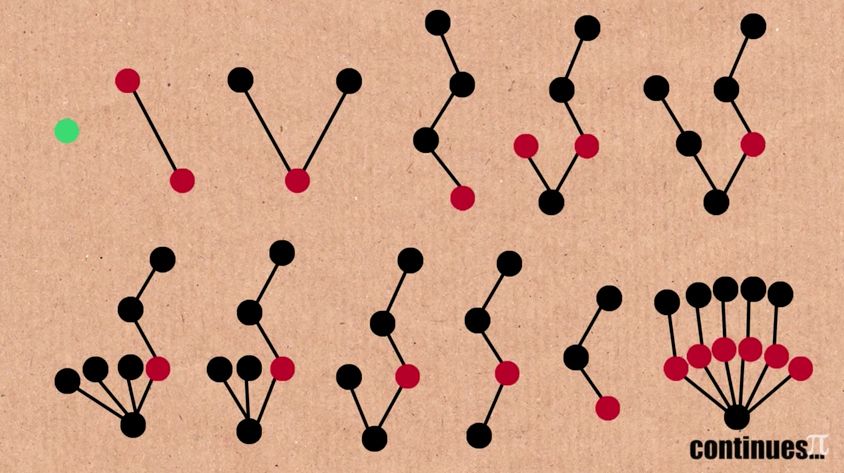
Wrap Your Head Around The Enormity Of The Number Tree 3

From 1 000 000 To Graham S Number Wait But Why

Conway Chained Arrow Notation Wikipedia

Tree Vs Graham S Number Numberphile Youtube

From 1 000 000 To Graham S Number Wait But Why

Tree 3 Is A Big Number I Mean Really Big Josh Kerr

Checkmate Scientists Tumblr

Tree Vs Graham S Number Numberphile Youtube

Tree Vs Graham S Number Numberphile Youtube

Too Big To Write But Not Too Big For Graham Plus Maths Org

How Big Is The Number Tree 3 Let Us See How Big A Forest Can We Grow By Priyabrata Biswas Towards Data Science

Tree Sequence Googology Wiki Fandom

Tree 3 Vs Rayo S Number Youtube

How Do We Know Tree 3 Is Bigger Than Graham S Number Youtube

Bluefin Tuna Phylogeny

Graham S Number Googology Wiki Fandom

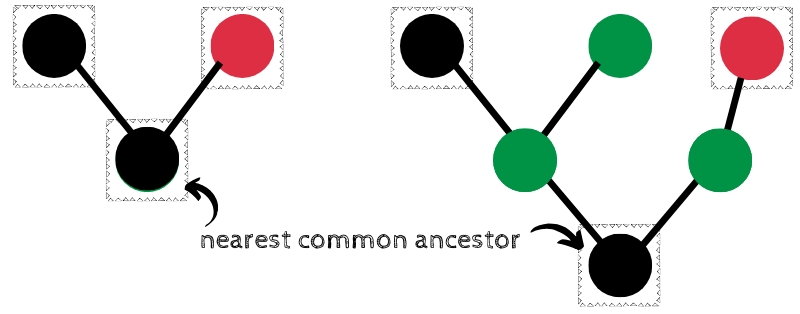
How Big Is The Number Tree 3 Let Us See How Big A Forest Can We Grow By Priyabrata Biswas Towards Data Science

Pentation Wikipedia

Tree Vs Graham S Number Numberphile Youtube

Tree 3 Is A Big Number I Mean Really Big Josh Kerr

How Big Is The Number Tree 3 Let Us See How Big A Forest Can We Grow By Priyabrata Biswas Towards Data Science

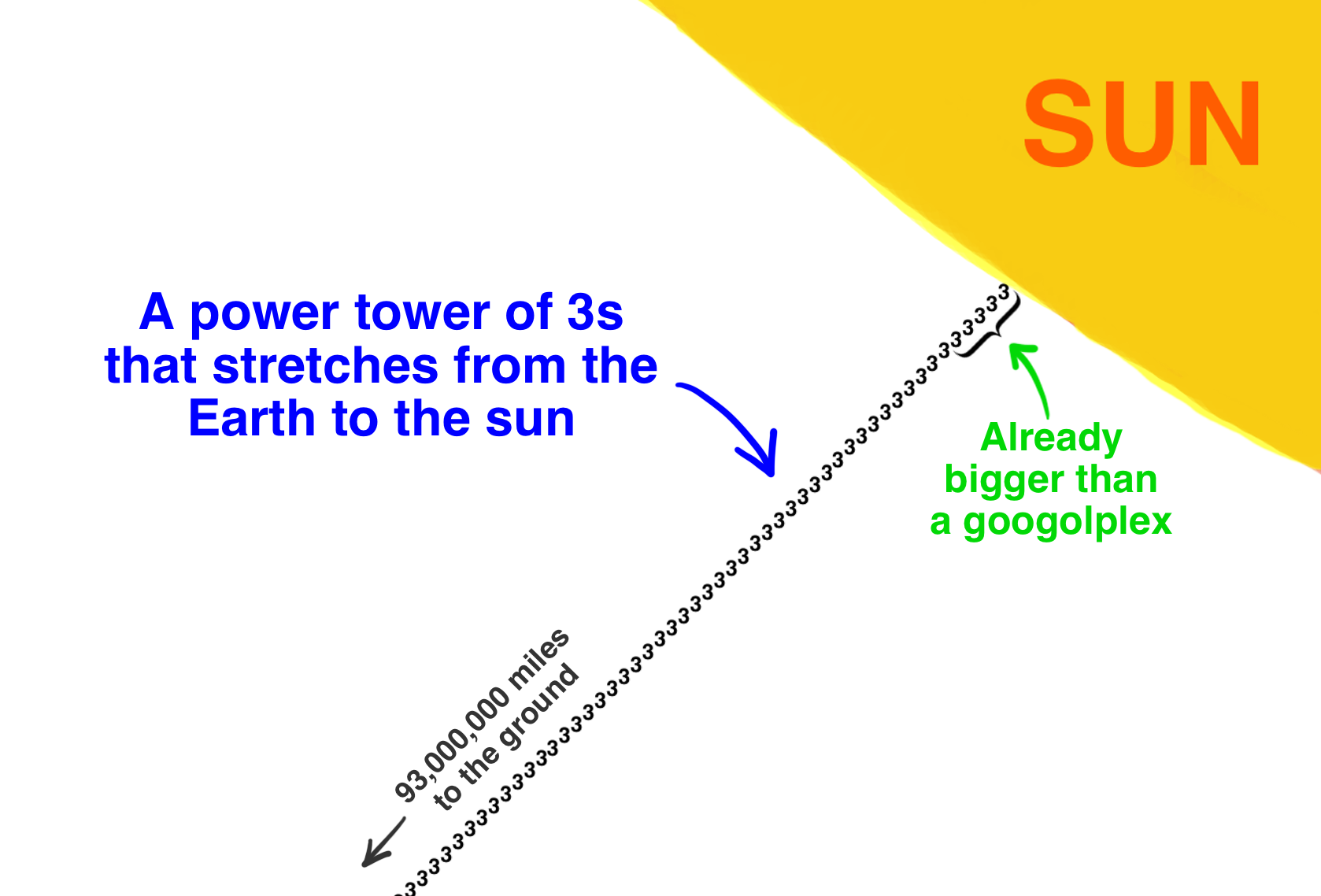
From 1 000 000 To Graham S Number Wait But Why

Tree Vs Graham S Number Numberphile Youtube

1716 Graham Court Pryor Ok Mcgraw Realtors

Www2 Palomar Edu Pages Math Files 17 12 2 E Finitely Big Numbers Key Pdf

How Many Zeros In A Million Billion And Trillion

Tree Vs Graham S Number Numberphile Youtube

From 1 000 000 To Graham S Number Wait But Why

Is It Possible To Write Graham S Number Digitally Quora

How Big Is Tree 3 Quora

Wrap Your Head Around The Enormity Of The Number Tree 3

Graham S Number Wikipedia

Graham S Number Is Too Big To Explain How Big It Is The Science Explorer

How Do We Know Tree 3 Is Bigger Than Graham S Number Youtube

How Big Is The Number Tree 3 Let Us See How Big A Forest Can We Grow By Priyabrata Biswas Towards Data Science

Tree 3 Is A Big Number I Mean Really Big Josh Kerr

Tree 3 Is A Big Number I Mean Really Big By Josh Kerr Black Cat Medium

Kefit 1 14 Scg 13 Bad At Fangames 2 15 Tree 3 Bad At Fangames 3 17 Graham S Number Bad At Fangames Progress Is Always Nice Tho T Co Vi9v86krur

Tree Of Life Biology Wikipedia

Wrap Your Head Around The Enormity Of The Number Tree 3

Ronald Graham Wikipedia

How Many Zeroes Are There In A Googolplexian Quora

From 1 000 000 To Graham S Number Wait But Why

From 1 000 000 To Graham S Number Wait But Why

Q Tbn And9gctm7i4f1olkwqwevqngl Chmja6dkohkbxpd7tibt5xmyhnfuda Usqp Cau

Wrap Your Head Around The Enormity Of The Number Tree 3

Golf A Number Bigger Than Tree 3 Code Golf Stack Exchange

From 1 000 000 To Graham S Number Wait But Why

2 7 Graham S Number Pointless Large Number Stuff

Http Www2 Math Ou Edu Jalbert Courses Projects Pdf

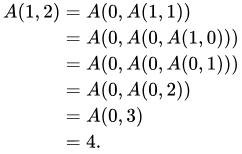
The Fast Growing Hierarchy Beyond Extreme Large Numbers By Vernieri An Introduction On Googology Medium

Image Yeah Tree 3 Is Certainly Larger Than Graham S Number Unexpectedfactorial

Tree 3 Funny Maths Graham S Number Large Graph Theorem Kruskal Seed Physics Ari Ebay

Tree Sequence Googology Wiki Fandom

How Have Mathematicians Determined Tree 3 To Be Far Larger Than Graham Number Quora

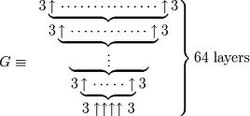
Graham S Number Googology Wiki Fandom

From 1 000 000 To Graham S Number Wait But Why

Tree 3 Funny Maths Graham S Number Large Graph Theorem Kruskal Seed Physics Ari Ebay

Q Tbn And9gcqztdsbnk8wuoxknrfs Arjtzk8634 Nr Npwghtqjjukoulfow Usqp Cau

How Big Is Graham S Number Feat Ron Graham Youtube

Tree 3 Is A Big Number I Mean Really Big Josh Kerr

Is Tree 3 Bigger Than Graham S Number Quora

What Is Bigger Than Astronomical The Magnificent Nature

Too Big To Write But Not Too Big For Graham Plus Maths Org

Graham S Number Wikipedia

From 1 000 000 To Graham S Number Wait But Why

Tree Vs Graham S Number Numberphile Youtube

Too Big To Write But Not Too Big For Graham Plus Maths Org

Beyond Infinity Number Comparison Youtube

The Most Massive Numbers In Existence Live Science

Too Big To Write But Not Too Big For Graham Plus Maths Org

Incoming Term: tree(3) vs graham's number,